Construisez un cadre

Par Daniel Maignan

Nous savons qu’il est possible d’utiliser un cadre pour recevoir les ondes radioélectriques à la place d’une antenne.  Avec ce genre de collecteur d'ondes, l’entrée du récepteur se trouve connectée à un circuit électriquement fermé et le signal capté résulte uniquement du courant haute fréquence induit par la composante magnétique du champ radioélectrique. Cet article fait appel à quelques développements mathématiques de base qui sont destinés à asseoir l’exposé.

We know that it is possible to use a loop instead of a wire antenna for receiving radio waves. With this type of setup, the receiver input is connected to an electrically closed circuit. Consequently, the signal received results entirely from the high frequency current induced by the magnetic component of the electromagnetic field. This article covers some mathematical fundamentals aimed at grounding the subject .

Les anciens cadres à air de grand format se composaient en général d’un enroulement fractionné dont les sections peuvent être couplées en série pour les grandes ondes et en parallèle pour les petites ondes. Le cadre est accordé par un condensateur variable. Pour sa confection, il sera nécessaire de suivre les étapes indiquées ci-dessous. Nos lecteurs un peu fâchés avec les mathématiques pourront laisser de côté toutes les démonstrations, en seulement tenant compte des données pour sa construction aux § 3 et 4.

1) Association des enroulements:

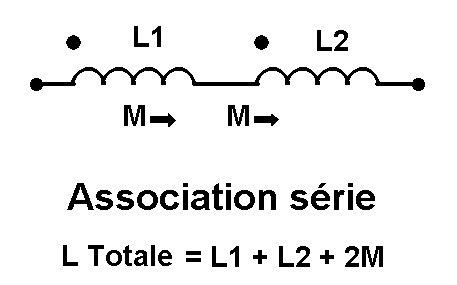
Il est indispensable d’éviter les « bouts morts » et dans cette réalisation, pour la gamme des GO, les deux enroulements L₁ et L₂ couplés par l’induction mutuelle M sont en série (figure 1) et en parallèle pour la gamme  des PO (figure 2). En série avec un couplage positif (M positif), l’inductance totale résultante est L_T:

                                                        L_T = L₁ + L₂ + 2M    (1)

         Figure 1 - Enroulements en série, couplage positif

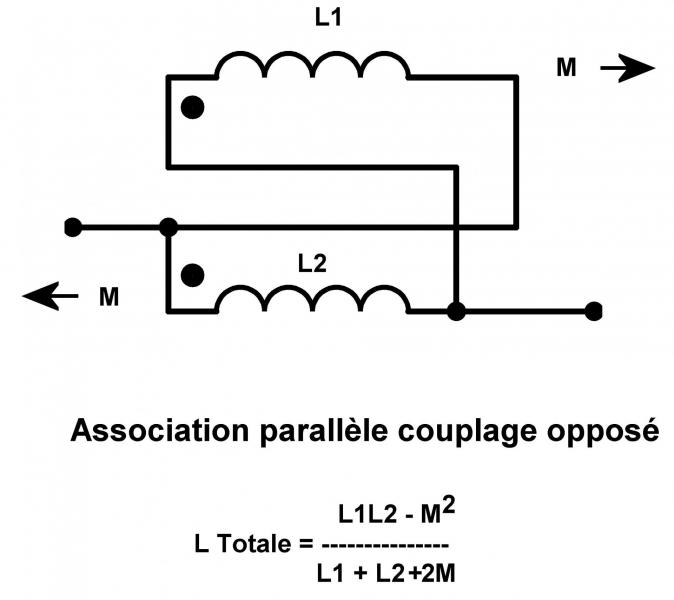
Les enroulements en parallèle donnent une nouvelle valeur d’inductance résultante L_T’, avec au dénominateur le terme 2M qui est positif ou négatif, selon le sens du couplage. Celui-ci est positif quand le couplage est négatif.

                                                                    L₁L₂ – M²

                                                         L_T’ =  ---------------    (2)

                                                                  L₁ + L₂ ± 2M

    Figure 2 - Enroulements en parallèle, couplage négatif.

On se  base sur une valeur de l’induction mutuelle M de l’ordre de 0,2 à 0,5 µH et l’on veut couvrir les gammes GO et PO avec notre cadre en l’accordant avec un condensateur variable de 500 pF.

2) Procédure de mesure, les capacités parasites :

Les cadres à air grand modèle ont une surface importante et les capacités parasites entre spires ont une valeur non négligeable dont il faut tenir compte. La capacité totale d’accord du cadre C_T sur une fréquence donnée est dans la réalité la somme de la capacité du condensateur externe C_ext plus les capacités parasites C_p.

                                                      C_T  = C_ext  + C_p      (3)

La capacité parasite peut atteindre plusieurs dizaines de pF.

2b) Cahier des charges:

Déterminons le cahier des charges à l'aide de la formule de Thomson F = 1/(2π√LC.  

La construction est réalisée avec deux enroulements L₁ et L₂ et un condensateur de 500 pF max.

On a donc:

-GO: inductance totale L_T requise en mettant en série L₁ et L₂: L_T = 1,9 mH (figure 1).    

-PO: inductance totale L_T’ requise en petites ondes, avec mise en parallèle de L1 et L2 en couplage négatif  (figure 2): L_T’ = 0,15 mH. 

-Induction mutuelle : M = 0,25 mH.  

-Capacités parasites (estimées) du cadre : 30 pF environ en PO et 25 pF environ en GO.  

-Capacité maximum du CV : 500 pF.        

-Capacité résiduelle mesurée sur le CV totalement ouvert: 32pF.

Les données sont résumées dans le tableau ci-dessous.

• 2c) Le calcul détaillé des inductances L₁ et L₂ à l’aide des formules (1) et (2) est donné ci-dessous:

3) Construction, dimensions mécaniques du cadre :

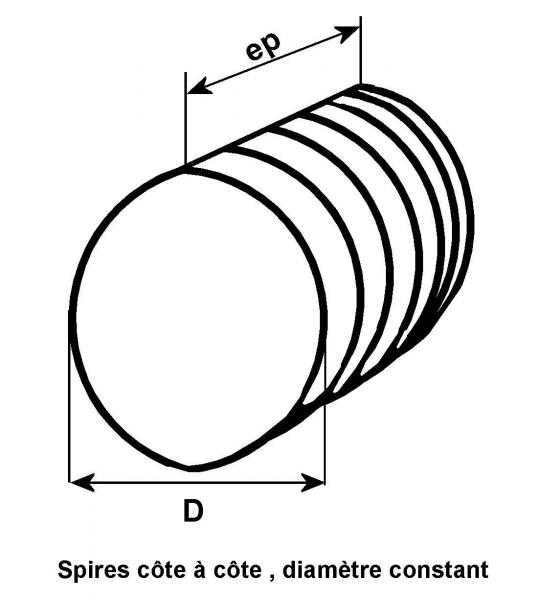
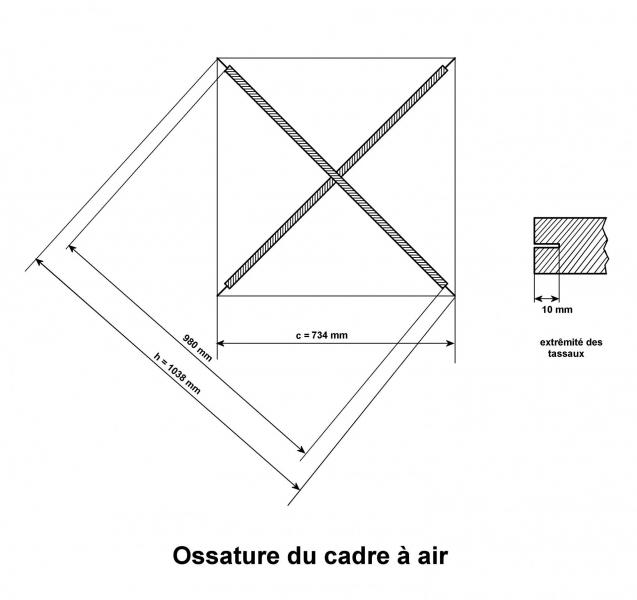
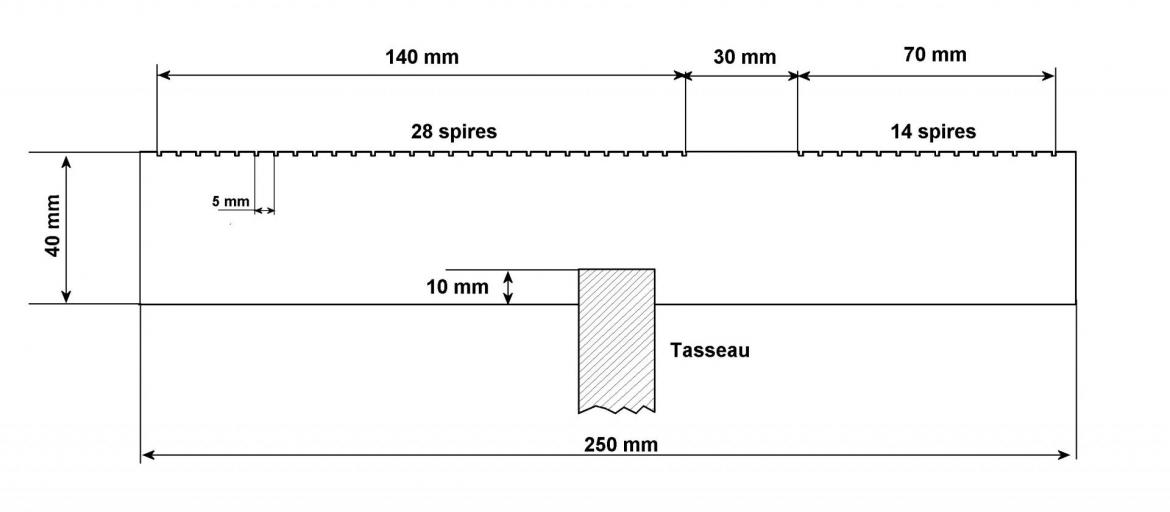
On adopte la technique des bobinages à spires égales de la figure 3. L’ossature est constituée de deux tasseaux croisés de 980 mm de longueur.

A l’aide d’une scie égoïne, on pratique aux quatre extrémités une fente de 10 mm de profondeur. Celle-ci est ensuite élargie et enduite de colle afin de recevoir le peigne support du fil (figure 4). Les quatre peignes sont réalisés en matière isolante. Un espace de 30 mm entre L1 et L2, qui a été déterminé expérimentalement, correspond, avec les valeurs d’inductances considérées, à une induction mutuelle de 0,25 mH environ (figures 5 et 6).

                  Figure 3 - Méthode d'enroulement à spires égales

                                           Figure 4 - Ossature

  Figure 5 - Croquis d'un peigne et de sa position sur un bras de l'ossature

                      Figure 6 - Photo d'un peigne avec les deux enroulements

En incluant les peignes, on obtient des spires de 73,4 cm de côté, d’où un carré de surface  S = 73,4 x 73,4 = 5387,56 cm². On recherche le diamètre D du cercle dont la surface est équivalente, à l’aide de la formule du cercle: S = πD²/4 :

                                        D = √ (4S/π) = √ (4 x 5387,56/3,14) =  82,84 cm.

3a) Calcul du nombre de spires pour L₁ et L₂ :

On a donc un cercle de diamètre équivalent D = 82,84 cm et on prend pour L₁ : ep  = 14 cm et pour L₂ : ep = 7 cm (approximativement, valeurs peu critiques dont l’influence est faible dans la formule, car ep < D). Le nombre de spires est obtenu par la formule de Nagaoka:

1^er cas : le bobinage comporte des spires égales bobinées côte à côte (se reporter à la figure 4)

L’inductance est donnée par la formule de Nagaoka :

                                                             L = Kn²D 10^-3        (4)

                                                                                  100

    Et dans notre cas, le coefficient K est  =   ----------------      (5)

                                                                        4 + (11.ep) /D

avec : L = inductance en µH

           n = nombre de spires

           ep= épaisseur (ou largeur) de l’enroulement en cm.

           D= diamètre des spires en cm.

- Calcul du nombre de spires n1 de L₁ :

                                                                           100                         

Appliquons la formule de (5) : K_L1 = ---------------------------  = 17

                                                              4 + (11 x 14)/82,4          

Avec la formule (4) on a : n₁ = √ (1077 x 10³/ 17 x 82,4) ≈ 28 spires

- Nombre de spires n2 de L₂ :

                                                                    100

Appliquons la formule (5) : K_L2 = ----------------------------  = 20,26

                                                           4 + 11 x (7/82,4)   

Avec (4) on a : n₂ = √ (322 x 10³/ 20,26 x 82,4) ≈ 14 spires

3b) Confection des enroulements:

 Sur le peigne inférieur, quatre petits trous permettent de faire un tour mort pour arrêter le fil au début et à la fin.

On enroule L₂ en premier lieu et on mesure ensuite sa valeur, comme indiqué ci-dessous. Après cette opération, L₁ est enroulée dans le même sens.

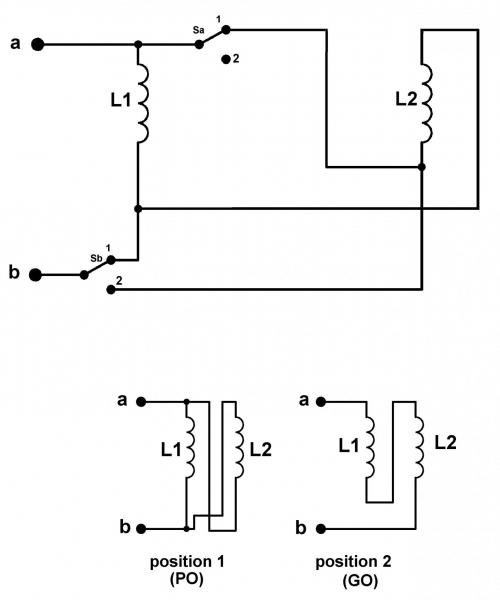
Figure 7 - Schéma électrique du cadre avec la commutation GO/PO

La figure 7 représente le schéma électrique du cadre avec la commutation PO/GO, le condensateur vient se connecter entre a et b.

4) Utilisation de ce cadre:

On peut l’utiliser de différentes manières : soit en le connectant aux prises antenne et terre du poste, à travers un cordon blindé de 50 cm de long, ou bien par couplage, le poste lui-même pourvu d’un cadre interne, est disposé à quelques dizaines de centimètres du cadre qui est accordé sur la fréquence à écouter (ou à l’intérieur du cadre, si c’est un poste portatif). Avec ce procédé de couplage, les résultats sont spectaculaires!

5) Mesures et validité des calculs:

Il faut souligner le fait que la mesure de L₂ doit être effectuée en premier, avant de bobiner L₁, car en raison du couplage, chaque mesure individuelle est influencée par l’élément couplé. (surtout la mesure de L₂ est influencée par le couplage avec L₁).

Pour vérifier les calculs, les mesures ont été effectuées avec un pont d’impédance Boonton (Rx meter 250A) et sont détaillées dans le tableau ci-dessous:

Pour chaque inductance, on effectuera ensuite deux essais :

-une mesure de résonance avec condensateur d’accord externe dans la bande correspondante.

-une mesure de la fréquence de résonance propre pour définir la capacité parasite C_p.

Daniel Maignan/F6HMT

Bibliographie :

L’Encyclopédie Pratique de la Radio

Bulletin de l’AEA N°103 Lt de Vaisseau G. Malgorn

Les bobinages radio de Hugues Gilloux, Société des Editions Radio 1942

Apprenez la radio en réalisant des récepteurs de Marthe Douriau, Editions de la Librairie de la Radio 1957

Revue Toute la radio N°129 octobre 1948                                                                                    

Revues Le Haut-Parleur

Revues Radio-Constructeur

Revues Radio-Plans

Copyright TLR 2020 - Toute reproduction interdite sans autorisation de l'auteur.